自动控制原理基础-06-教材MATLAB例题整理

本篇对教材第二章到第五章的所有 MATLAB 例题进行了整理。部分代码与例题中的有所修改更正，并重新格式化。

第二章 微分方程与传递函数

例题1 绘制零-极点分布图

有一闭环控制系统，其传递函数为

$G_b (s) = \frac{2s^2 + 5s + 1}{s^3 + 2s^2 + 3s + 1}$

，要求绘制其零-极点分布图。

num = [2, 5, 1];
den = [1, 2, 3, 1];
pzmap(num, den);
sys = tf(num, den); % 传递函数
z = tzero(sys); % 由所有零点构成的列向量
p = pole(sys); % 由所有极点构成的列向量

TODO 图表

第三章 频率特性

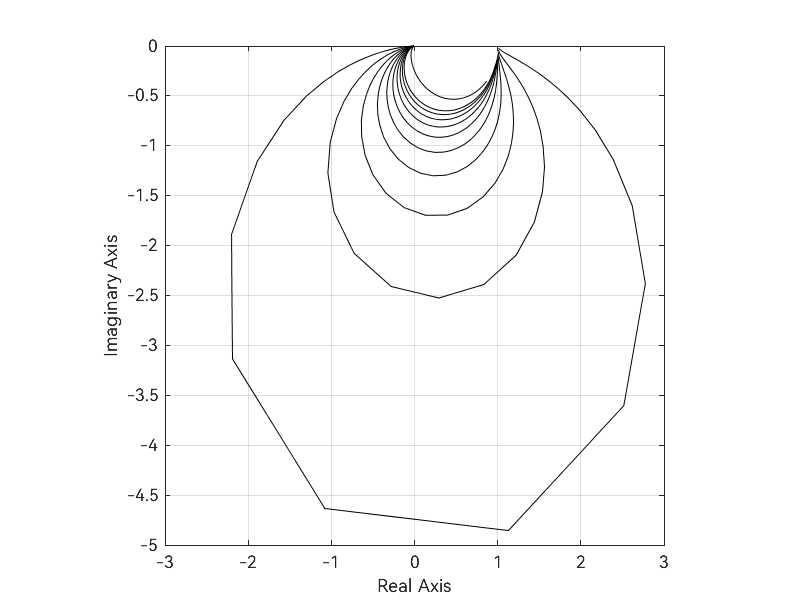
例题1 绘制奈奎斯特图（使用 plot）

有一系统传递函数为

$G(s) = \frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}$

，试画出该系统在不同阻尼比情况下的 Nyquist 图。

wn = 1; % 无阻尼自然振荡频率
zeta = [0.1:0.1:1, 2]; % 几种阻尼比
w = logspace(-1, 1, 100);
X = zeros(length(w), length(zeta));
Y = zeros(length(w), length(zeta));

for i = 1:length(zeta)
    dd = wn^4 + w.^4 + 2 * (2 * zeta(i)^2 -1) * wn^2 * w.^2;
    x = wn^2 * (wn^2 - w.^2) ./ dd;
    y = -2 * zeta(i) * wn^3 * w ./ dd;
    X(:, i) = x;
    Y(:, i) = y;
end

% 绘图
plot(X, Y, '-k')
axis('square') % 调整坐标轴：使用相同长度的坐标轴线。相应调整数据单位之间的增量。
grid on; % 绘制网格
xlabel('Real Axis') % x 轴标签
ylabel('Imaginary Axis') % y 轴标签

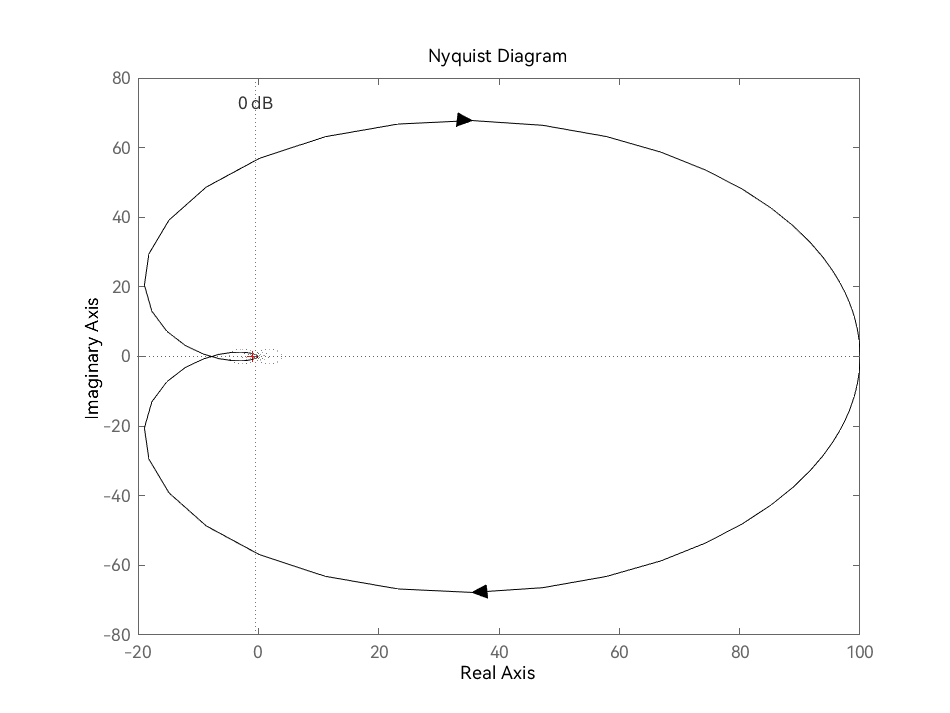
例题2 绘制奈奎斯特图（使用 nyquist ）

有一系统的开环传递函数

$G(s) = \frac{1000}{(s+1)(s+2)(s+5)}$

，试画出其奈奎斯特图。

G = tf(1000, conv([1, 1], conv([1, 2], [1, 5])));
nyquist(G, '-k')
% 更正教材代码错误： nyquist 图并不支持 axis 命令
grid on % 绘制网格

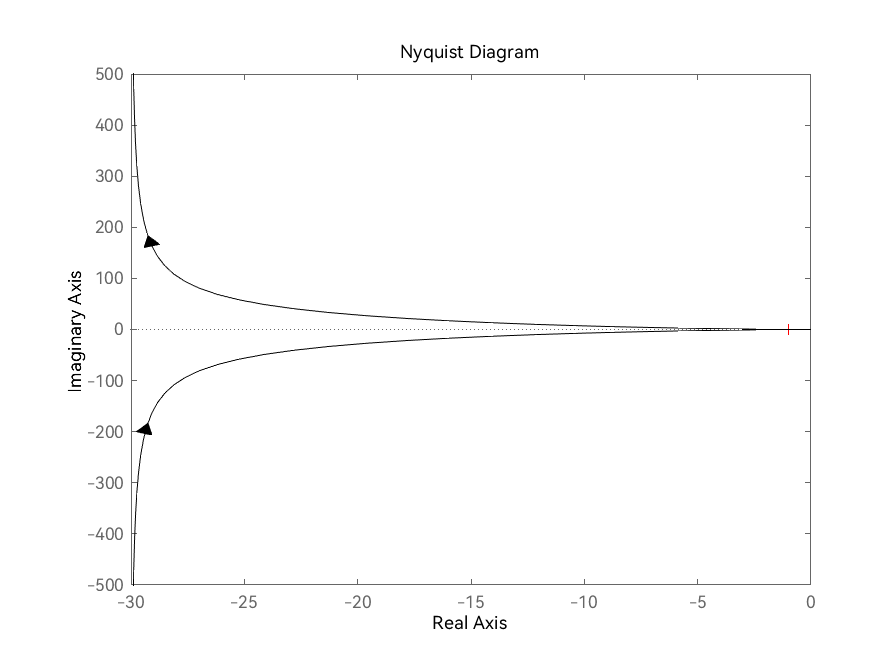
例题3 绘制奈奎斯特图（使用 nyquist ）

已知某系统的开环传递函数为

$G(s) = \frac{10}{s(3s + 1)}$

，试绘制其奈奎斯特图。

num = 10; % 分子
den = [3, 1, 0]; % 分母
nyquist(num, den, '-k')

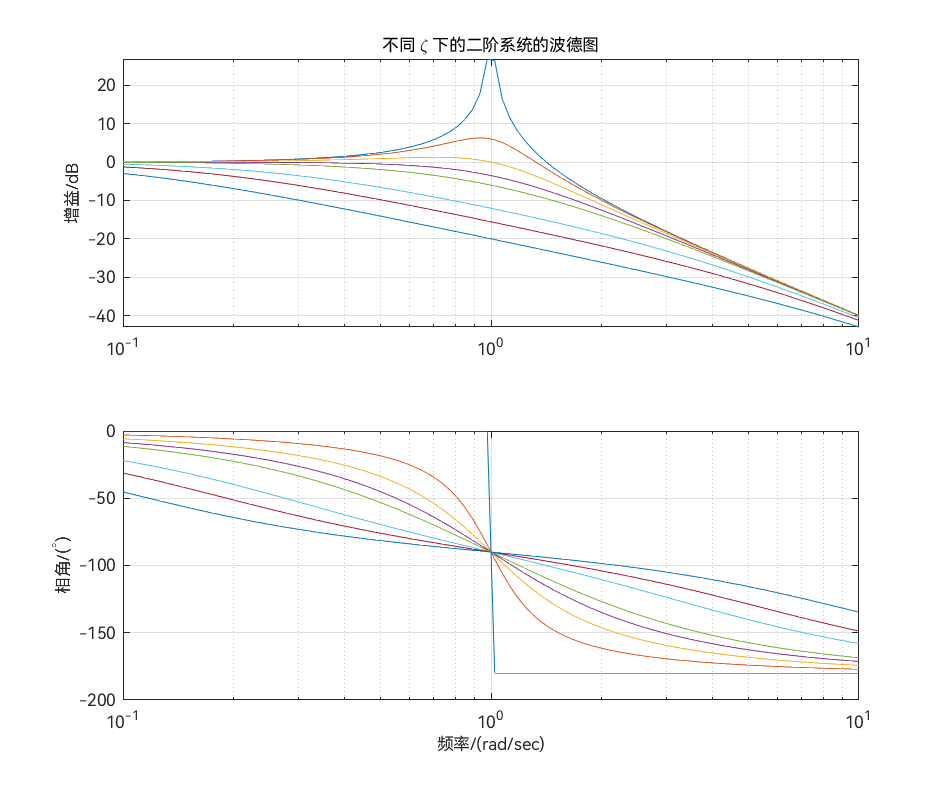
例题4 绘制波德图（使用 subplot）

传递函数为

$G(s) = \frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}$

的二阶系统，试用 MATLAB 语言画出其波德图。

经计算可得其幅频特性和相频特性分别为

$A(\omega) = \frac{\omega_n^2}{\sqrt{(\omega_n^2 - \omega^2)^2 + 4\zeta \omega_n^2 \omega^2}}$

$\varphi(\omega) = - \arctan \Big( \frac{2 \zeta \omega_n \omega}{\omega_n^2 - \omega^2} \Big)$

wn = 1; % 无阻尼自然振荡频率
zetas = [0:0.25:1, 2, 3, 5]; % 几种阻尼比
w = logspace(-1, 1, 100);
mm = zeros(length(w), length(zetas));
pp = zeros(length(w), length(zetas));

for i = 1:length(zetas)
    m = wn^2 ./ sqrt((wn^2 - w.^2).^2 + 4 * zetas(i)^2 * wn^2 * w.^2);
    p = atan2(-2 * zetas(i) * wn * w, wn^2 - w.^2);
    pp(:, i) = 180 * p' / pi;
    mm(:, i) = 20 * log10(m');
end

% 绘图
% 对数频率特性图
subplot(2, 1, 1) % 绘制第一个子图
semilogx(w, mm) % 半对数图（x 轴对数刻度，y 轴线性刻度）
grid on
ylabel('增益/dB')
title('不同 \zeta 下的二阶系统的波德图')
% 对数相频特性图
subplot(2, 1, 2) % 绘制第二个子图
semilogx(w, pp)
grid on
ylabel('相角/(^{\circ})')
xlabel('频率/(rad/sec)')

例题5 绘制波德图（使用 bode）

用 MATLAB 语言绘制传递函数为

$G(s) = \frac{3(0.5s + 1)}{(2.5s + 1)(0.025s + 1)}$

的系统的波德图。

G = tf(3 * [0.5, 1], conv([2.5, 1], [0.025, 1]));
bode(G, '-k') % 绘制波德图，指定线条颜色为黑色
grid on % 绘制网格

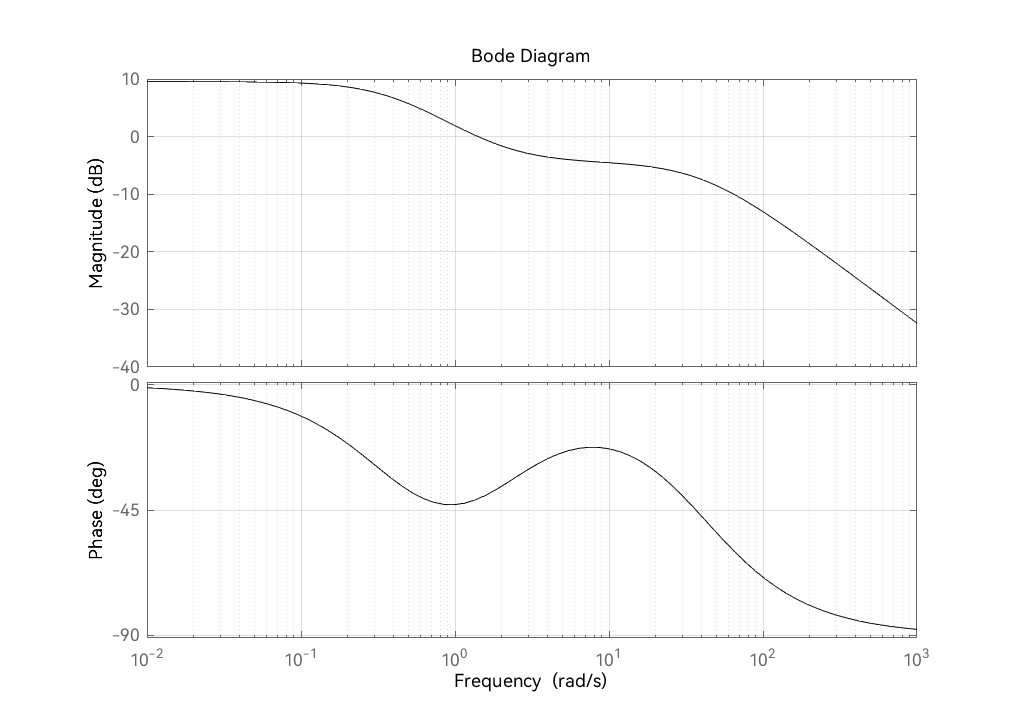
例题6 绘制波德图（使用 bode）

绘制传递函数为

$G(s) = \frac{5 (1 + 0.1s)}{s(1+0.5s)(1+0.012s+0.0004s^2)}$

的系统的波德图。

G = tf(5 * [0.1, 1], conv([1, 0], conv([0.5, 1], [0.0004, 0.012, 1])));
bode(G, '-k')
grid on

第四章 控制系统的稳定性分析

例题1 判别系统稳定性

系统的传递函数为

$G(s) = \frac{s^3 + 5s^2 + 20s + 20}{s^4 + 10s^3 + 25s^2 + 40s + 25}$

试用 MATLAB语言编程判别系统的稳定性。

G = tf([1, 5, 20, 20], [1, 10, 25, 40, 25]); % G 为传递函数
roots(G.den{1}) % G.den{1} 即为特征方程

% 由结果可知，该系统的特征方程的 4 个根均无正实部，所以该系统稳定

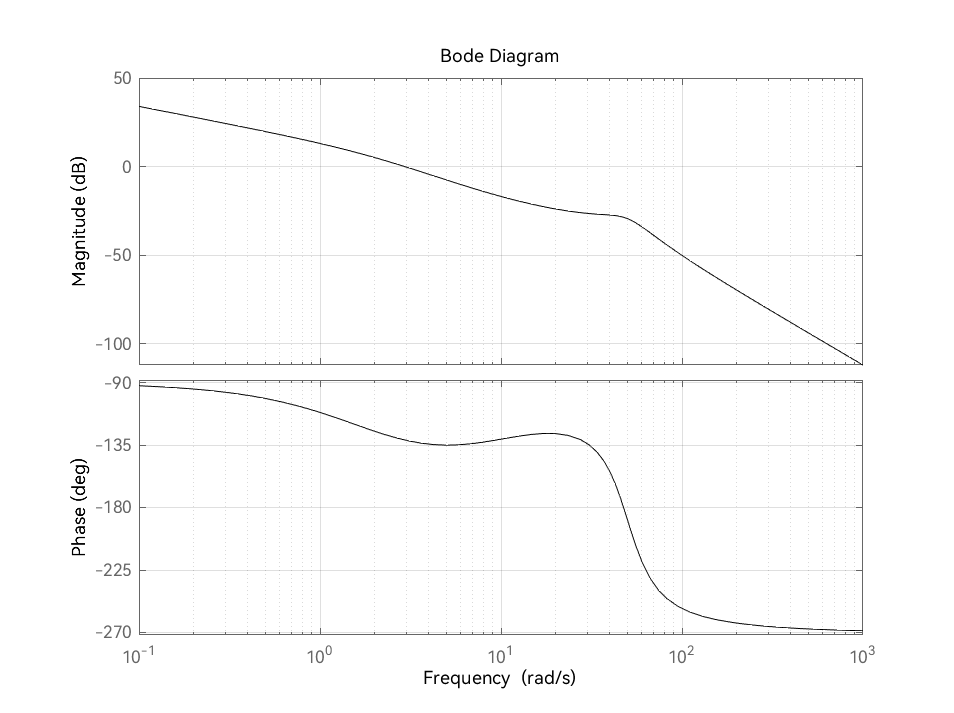
例题2 求幅值裕量、相位裕量（margin）

设控制系统的开环传递函数为

$G(s)H(s) = \frac{k}{s(s+1)(s+5)}$

当 $k=10$，$k=100$ 时，判断系统是否稳定？求系统的幅值裕量 $K_g$ 和相位裕量 $\gamma$

解：

由 $G(s)H(s) = \frac{k}{s(s+1)(s+5)}$ 的分母可知该系统开环稳定，将其化为标准环节的形式

$G(s) H(s) = \frac{K}{s(s+1)(\frac{s}{5} + 1)}$

当 $k = 10$ 时，程序如下

GH = tf(10, conv([1, 0], conv([1, 1], [1, 5])));
sys = feedback(GH, 1);

p = pole(sys); % 由所有极点构成的列向量
z = tzero(sys); % 由所有零点构成的列向量

n1 = length(find(real(p) > 0)); % 实部大于零的极点的个数
n2 = length(find(real(z) > 0)); % 实部大于零的零点的个数

if (n1 > 0)
    disp('系统不稳定！');
else
    disp('系统稳定！');
end

if (n2 > 0)
    disp('系统不是最小相位系统！');
end

[Gm, Pm, Wcg, Wcp] = margin(GH); % 以绝对单位返回 幅值裕量、相位裕量、分别对应的频率
PGm = num2str(20 * log10(Gm)); % 幅值裕量
PPm = num2str(Pm); % 相位裕量
disp(['系统的幅值裕量为 ', PGm]);
disp(['系统的相位裕量为 ', PPm]);

margin(GH) % 绘图

第五章 控制系统的时间响应及稳态误差分析

例1 绘制二阶闭环系统在不同阻尼比下的阶跃响应曲线

% 二阶闭环系统在不同阻尼比下的阶跃响应
% Step response of the second-order closed-loop system under different damping ratios


wn = 1; % 无阻尼自然振荡频率
zetas = [0:0.25:1, 2, 3, 5]; % 几种阻尼比
t = 0:0.1:12; % 时间
% 为编程方便，程序中输出量 x_o(t) 用 y 代替
yy = zeros(length(zetas), length(t)); % 存储各种阻尼比下输出量 y 的值的矩阵

% 计算各曲线上各点值
for i = 1:length(zetas)
    z = zetas(i);

    if z == 0 % 零阻尼
        y = 1 - cos(wn * t);
    elseif (z > 0 && z < 1) % 欠阻尼
        wd = wn * sqrt(1 - z^2);
        th = atan(sqrt(1 - z^2) / z);
        y = 1 - exp(-z * wn * t) .* sin(wd * t + th) / sqrt(1 - z^2);
    elseif z == 1 % 临界阻尼
        y = 1 - (1 + wn * t) .* exp(-wn * t);
    elseif z > 1 % 过阻尼
        lam1 = -z - sqrt(z^2 - 1);
        lam2 = -z + sqrt(z^2 - 1);
        y = 1 - 0.5 * wn * (exp(lam1 * t) / lam1 - exp(lam2 * t) / lam2) / sqrt(z^2 - 1);

    end

    yy(i, :) = y;
end

% 绘图
plot(t, yy)
title('二阶闭环系统在不同阻尼比下的阶跃响应')
xlabel('t')
ylabel('x_o(t)')
grid on

例题2 绘制系统的阶跃响应曲线

系统传递函数为

$G(s) = \frac{1}{s^2 + 0.4s + 1}$

试绘制该系统的阶跃响应曲线。

num = 1; % 分子
den = [1, 0.4, 1]; % 分母
G = tf(num, den); % 传递函数
step(G) % 阶跃响应曲线

例题3 电机调速

TODO