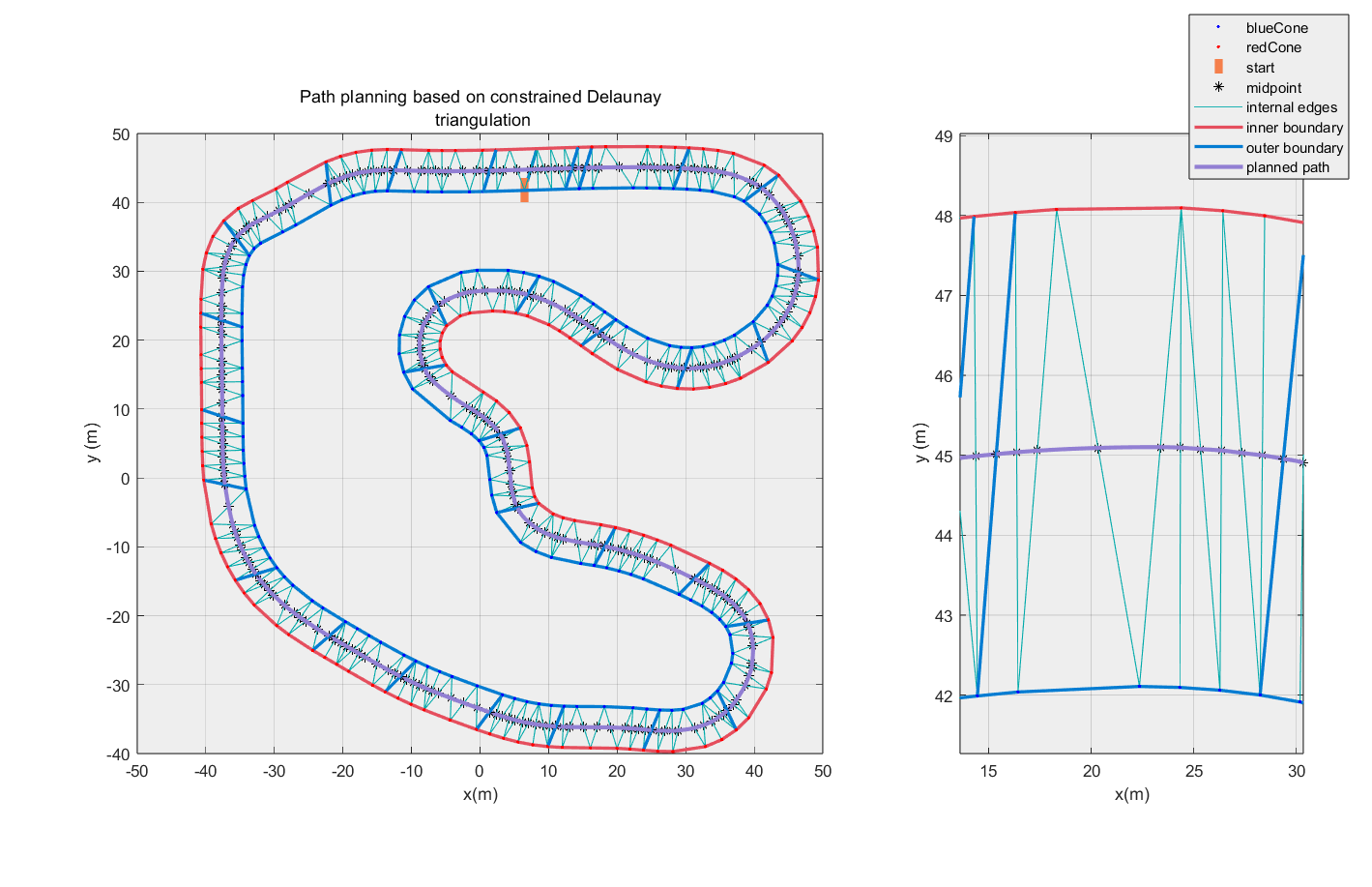
基于 Delaunay 三角剖分的 FSAE 路径规划算法

本文最后更新于 2023年3月6日 下午

本文为项目 FSAE-PathPlanning-Delaunay 之文档，完整代码见 https://github.com/muziing/FSAE-PathPlanning-Delaunay

引言

在 FSAE（大学生方程式赛车）无人车比赛中，赛车需要根据传感器返回的作为路径边界标识的交通锥桶的信息（颜色、位置坐标），进行路径规划，进而为下一刻的控制提供依据。良好的路径规划算法应能够根据离散的锥桶坐标，快速规划出一条光滑、连续、合理靠近车道中心线的目标路径。

Plan the path through the cones

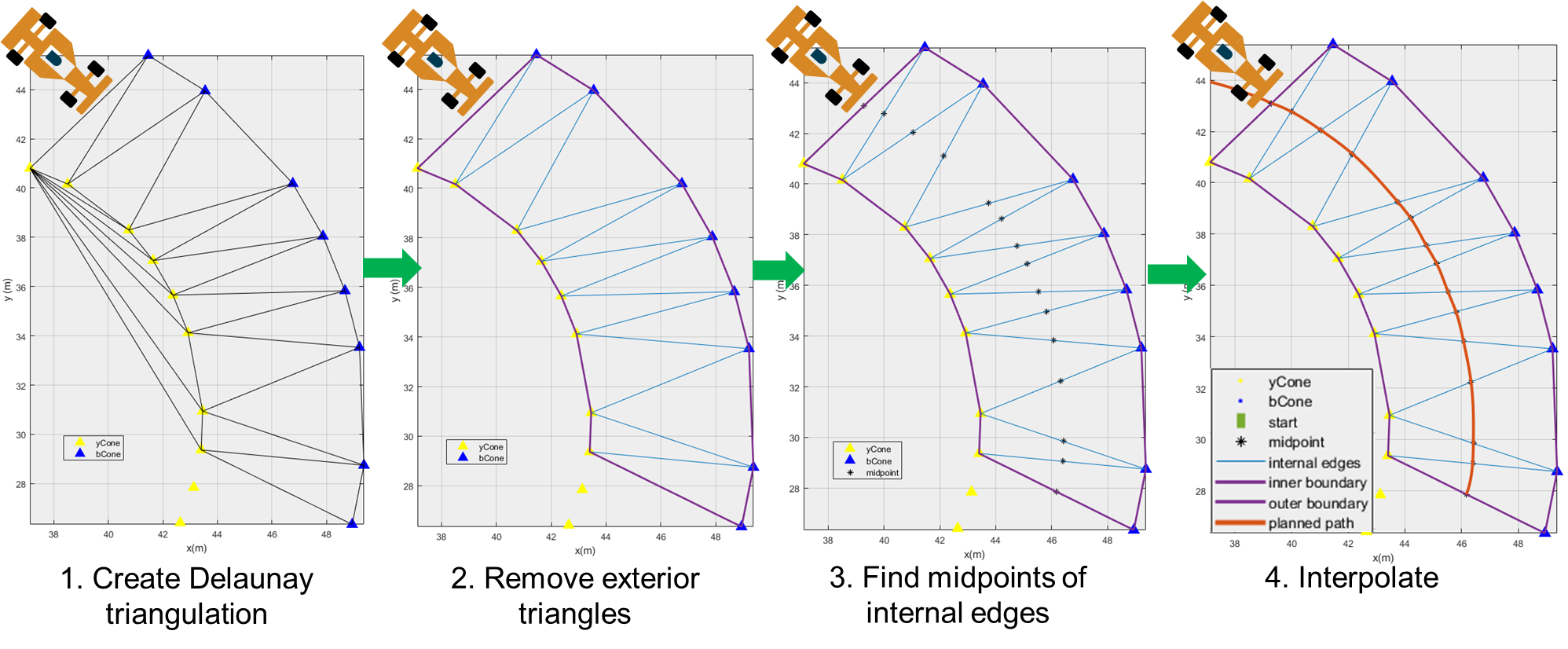
本文介绍了一种基于 Delaunay 三角剖分的路径规划算法：将锥桶位置视为离散点，构建 Delaunay 三角，然后以位于车道内部的那些三角形边的中点为依据进行插值，最终得到期望路径。经验证，该算法基本可以完成路径规划任务。

算法主要流程

背景知识：Delaunay三角剖分

创建Delaunay三角剖分

读取加载数据

首先从 CSV 文件中导入锥桶位置坐标。

CSV 数据示例如下，

1
2
3
4
5
6
7
8
9
num,type,x_coor,y_coor
1,2,8.29483356036796,47.8005083348189
2,2,10.2903642978411,47.8659036790991
3,2,12.2903853701921,47.9291209919643
...
152,11,6.49447171658257,41.7389113024907
153,11,8.49189149682204,41.8037451937836
154,11,10.4848751821667,41.8690573815958
...
  • 第一列为锥桶序号，内外侧锥桶已经分别按照赛道顺序排序
  • 第二列为锥桶类型（颜色），2 为外侧锥桶（蓝色，位于车辆行驶方向的左侧）、11 为内侧锥桶（黄色，位于车辆行驶方向的右侧）
  • 第三四列为 x 坐标与 y 坐标，单位为 [m]

编写 MATLAB 代码读取数据：

1
2
3
4
5
6
7
8
%% 加载锥桶坐标数据
conePosTable = readtable("cone_position_data.csv");
innerIndex = conePosTable.type == 11; % 内侧锥桶索引
innerConePosition = [conePosTable(innerIndex, "x_coor"), ...
                         conePosTable(innerIndex, "y_coor")];
outerIndex = conePosTable.type == 2; % 外侧锥桶索引
outerConePosition = [conePosTable(outerIndex, "x_coor"), ...
                         conePosTable(outerIndex, "y_coor")];

此时已将内、外侧锥桶的xy位置坐标分别存储在 innerConePosition 与 outerConePosition 两张 table 中。

数据预处理

然后需要将内外侧锥桶的坐标交替合并，得到将用于创建 delaunayTriangulation 对象的 P 矩阵。

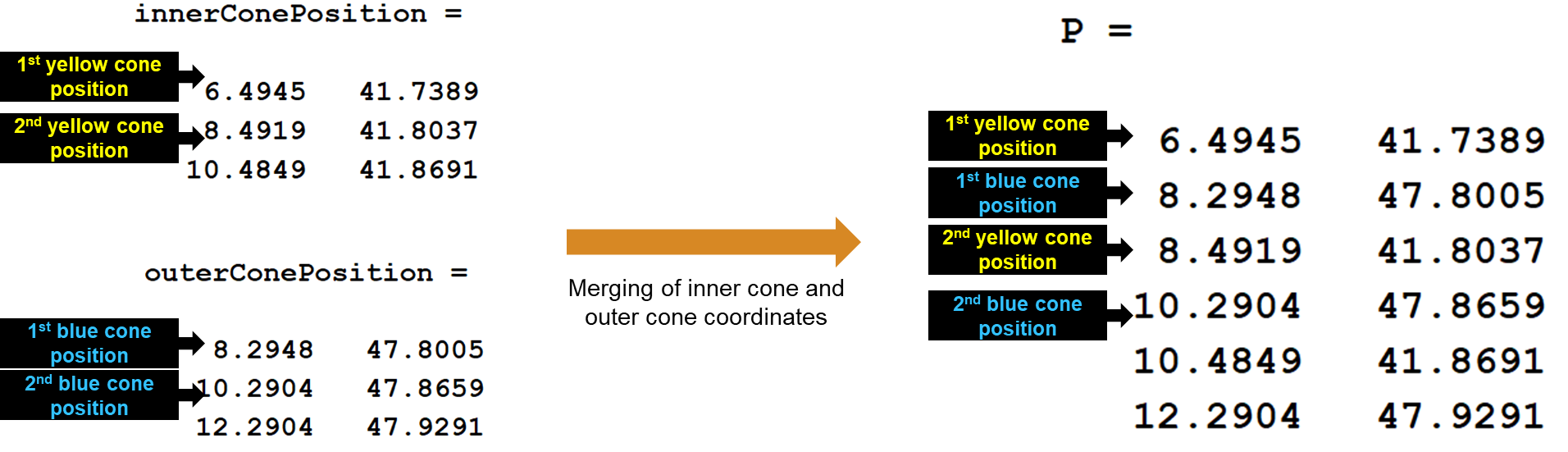
交替合并坐标

1
2
3
4
5
6
%% 数据预处理
[m, nc] = size(innerConePosition); % 内/外侧锥桶位置数据的size
P = zeros(2 * m, nc); % 初始化由内侧坐标与外侧坐标组成的 P 矩阵
% 将内外侧坐标交替合并
P(1:2:2 * m, :) = innerConePosition.Variables;
P(2:2:2 * m, :) = outerConePosition.Variables;

在真实场景中，安装在赛车上的传感器的感知范围是有限的，并不能一次获取所有锥桶位置。因此，设计一个变量 interval，用于控制每次规划时考虑的锥桶数量。（换言之，将整条赛道划分为若干个路段，每次只在一个路段内进行规划。）如图所示，若 interval = 4，则将基于每 4 个锥桶坐标创建 Delaunay 三角剖分。

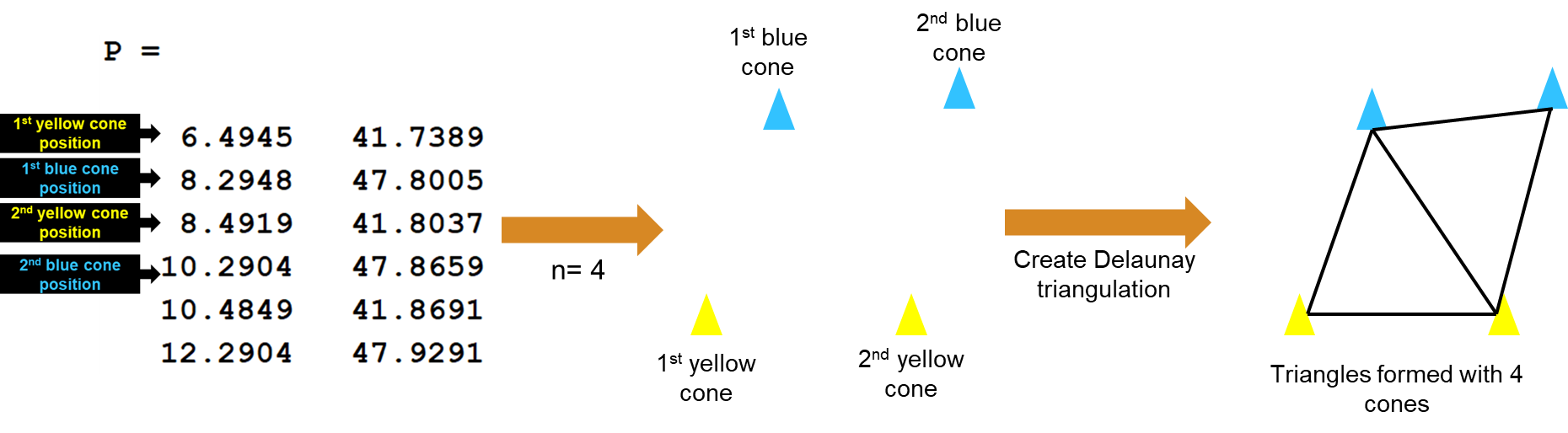
在一个路段内创建 Delaunay 三角剖分

1
2
3
4
5
interval = 10; % 每次规划时考虑的路段长度
interpolationNum = 100; % 插值点数量
pathCount = idivide(uint16(2 * m), interval, 'floor') * interpolationNum; % 最终规划路径坐标点个数
xPos = zeros(1, pathCount); % 数值向量 xPos，用于每次迭代后存储规划的 x 坐标
yPos = zeros(1, pathCount); % 数值向量 yPos，用于每次迭代后存储规划的 y 坐标

构建三角形

用一个 for 循环控制，每次循环中进行一个路段的路径规划，循环完成后即完成整条赛道的路径规划。注意此段之后代码的缩进，表明后续代码均在此循环体内：

1
2
for i = interval:interval:2 * m
    % 在每次循环中进行一个路段的路径规划，路段区间长度由interval控制

计算出属于该路段的坐标点集索引 pointIndex，P(pointIndex, :) 即为属于该路段的坐标。以此创建 delaunayTriangulation 对象 delaTria。

1
2
3
4
5
%% 构建 Delaunay 三角形
pointIndex = ((abs((i - 1) - interval)):i); % 属于该局部路段的点集的索引
delaTria = delaunayTriangulation(P(pointIndex, :)); % 为该路段的点集创建 Delaunay 三角剖分
delaTriaPoints = delaTria.Points; % 顶点坐标
[mc, ~] = size(delaTriaPoints); % size

Delaunay 三角剖分可视化：

1
2
3
4
5
6
7
8
9
10
11
% 绘制 Delaunay 三角剖分
figure(1)
triplot(delaTria, 'k')
grid on
ax = gca;
ax.GridColor = [0, 0, 0]; % [R, G, B]
xlabel('x(m)')
ylabel('y (m)')
set(gca, 'Color', '#EEEEEE')
title('Delaunay Triangulation')
hold on

Figure_1

移除外部三角形

如图所示，在进行三角剖分时，可能会创建出落在赛道之外的三角形，进而导致后续产生错误的路径。因此需要通过施加约束边界 C 去除这些外部三角形。

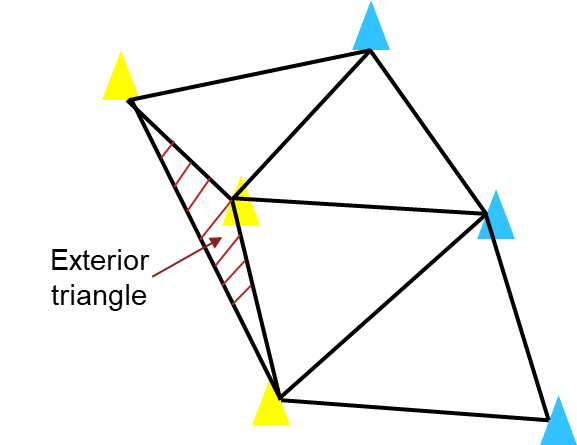
外部三角形

定义约束

约束边界 C 是一个由约束边的顶点 ID 所组成的两列矩阵，它的每一行对应一条约束边，其中：

  • C(j, 1) 为第 j 条约束边起始顶点的 ID
  • C(j, 2) 为第 j 条约束边末端顶点的 ID

下图显示了由矩阵 C = [2 1;1 3;3 5;5 6;2 4;4 6] 所定义的约束边界。

约束边界C

通过如下代码生成约束边界矩阵 C：

1
2
3
4
5
6
7
8
9
10
11
12
13
%% 移除外部三角形
% 获取约束边界 C
if rem(interval, 2) == 0
    % 当区间为偶数时的内外侧约束
    cIn = [2, 1; (1:2:mc - 3)', (3:2:(mc))'; (mc - 1), mc];
    cOut = [(2:2:(mc - 2))', (4:2:mc)'];
else
    % 区间为奇数时的内外侧约束
    cIn = [2, 1; (1:2:mc - 2)', (3:2:(mc))'; (mc - 1), mc];
    cOut = [(2:2:(mc - 2))', (4:2:mc)'];
end

C = [cIn; cOut]; % 连接约束边界的矩阵

创建带有约束的 Delaunay 三角剖分

定义约束后，使用 delaunayTriangulation 对象创建二维 Delaunay 三角剖分：

1
TR = delaunayTriangulation(delaTriaPoints, C); % 带约束的 Delaunay 三角剖分

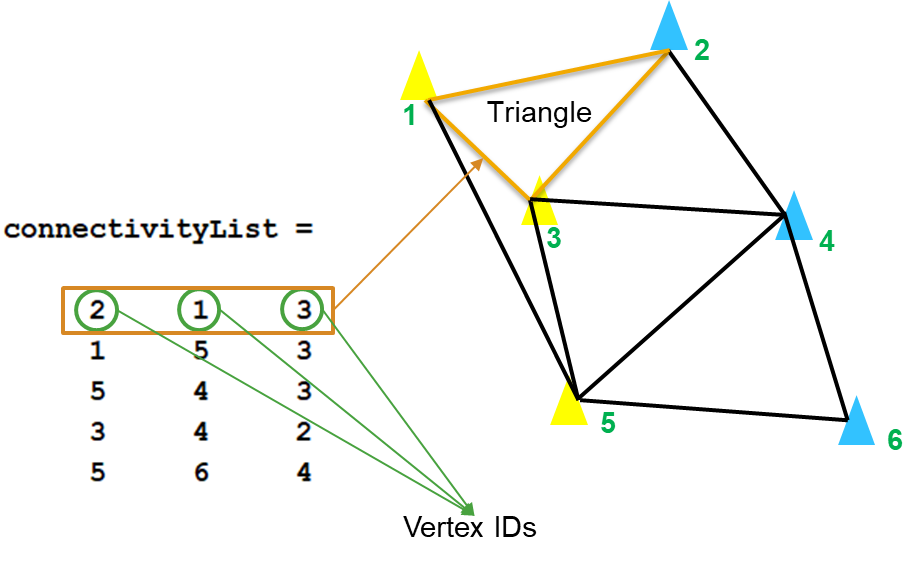
在继续下一步之前，需要介绍一下 delaunayTriangulation 的 Connectivity List（连接列表）属性。该属性将在后续步骤中被使用，实现通过排除外部三角形来创建新的三角剖分。

根据文档，一个三角剖分（如 DT）的连接列表是一个具有以下特征的矩阵：

  • DT.ConnectivityList 中的每个元素是一个顶点 ID
  • 每一行中的顶点构成了三角剖分中的一个三角形
  • 行号对应于该行所表示的一个三角形 的ID

例如，在下图中，第一行的 [2 1 3] 表示三角剖分后产生的第一个三角形。

连接列表

在了解连接列表的含义之后，让我们看看如何利用带约束的 Delaunay 三角剖分 TR 的连接表来移除外部三角形。

1
TRC = TR.ConnectivityList; % 三角剖分连接矩阵

获得连接矩阵 TRC 后，要删除构成外部三角形的那些行。如下图示意，第二行 [1 5 3] 代表的是一个外部三角形。

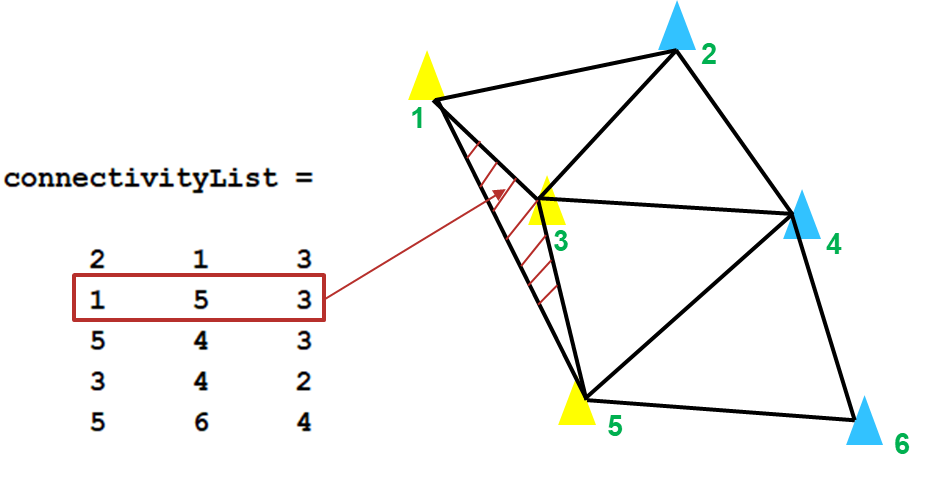
连接列表矩阵中的外部三角形

调用 delaunayTriangulation 对象的函数，可以实现各种拓扑与几何查询。在此处使用对象函数 isInterior 来检查每一行 ID 的三角形是否在有界几何区域内。该函数返回一个由逻辑值（布尔值）所组成的列向量：如果第 n 个逻辑值为 true，则三角剖分中的第 n 个三角形在约束区域 C 内，否则该三角形在约束区域 C 外，为外部三角形。

isInterior对象函数处理结果

1
2
TL = isInterior(TR); % 三角形是否在约束边界内的逻辑值
TC = TR.ConnectivityList(TL, :); % 三角剖分连接矩阵（去除外部三角形）

通过上述处理，获得了不包含外部三角形的新的连接列表矩阵 TC。然后依据 TC，从 delaTriaPoints 包含的点中创建一个新的二维三角剖分：

1
2
3
4
%（可选步骤） 使连接矩阵的行按升序排列，确保三角形按递进顺序连接
[~, pt] = sort(sum(TC, 2));
TS = TC(pt, :); % 按行升序的连接矩阵
finalTria = triangulation(TS, delaTriaPoints); % 基于已排序的连接矩阵创建三角剖分

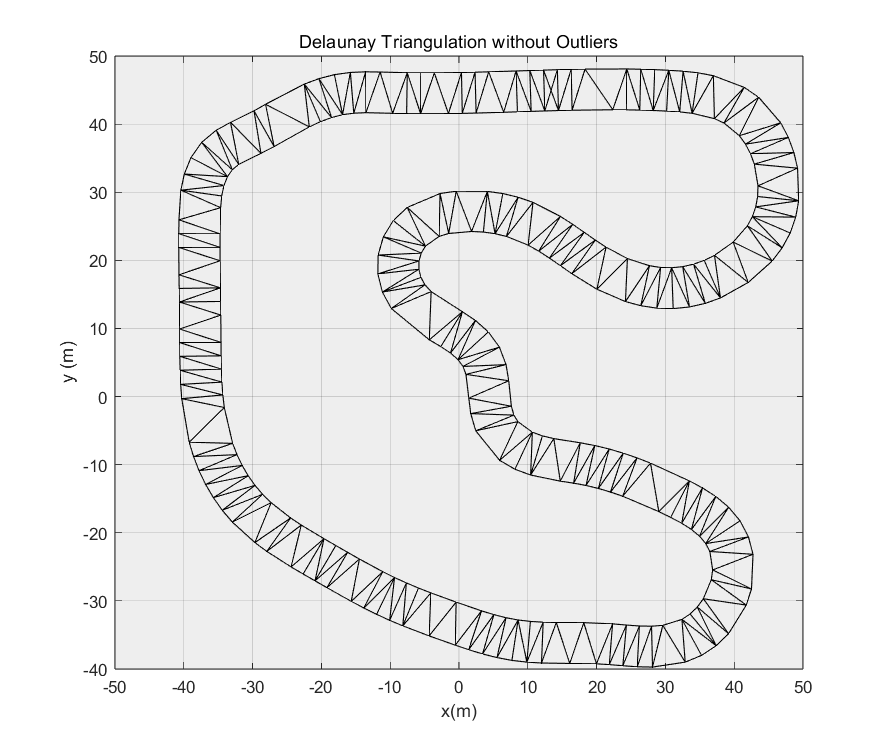
绘图，可视化观察可知，已经成功去除了外部三角形。

1
2
3
4
5
6
7
8
9
10
11
% 绘制去除外部三角形的 Delaunay 三角剖分
figure(2)
triplot(finalTria, 'k')
grid on
ax = gca;
ax.GridColor = [0, 0, 0]; % [R, G, B]
xlabel('x(m)')
ylabel('y (m)')
set(gca, 'Color', '#EEEEEE')
title('Delaunay Triangulation without Outliers')
hold on

Figure_2

获取中点与平滑处理

获取内部边中点

如下图所示，寻找所有位于车道内部的三角形边的中点，连接这些中点即为初步规划出的路径：

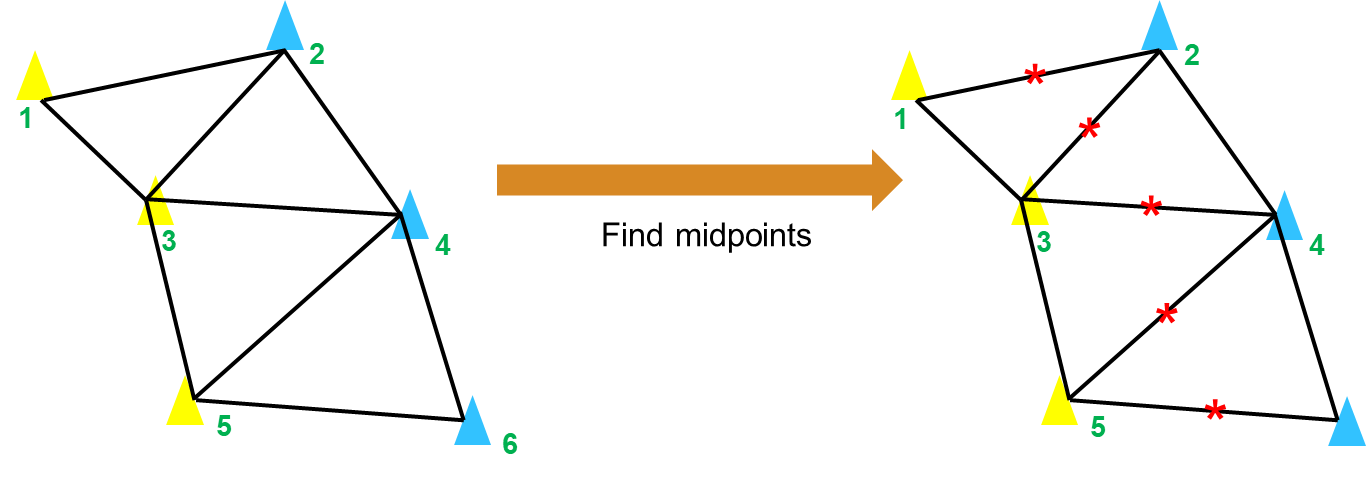
找到内边中心点

1
2
3
4
5
6
7
8
9
10
11
12
13
%% 寻找内边中心点
xPoints = finalTria.Points(:, 1);
yPoints = finalTria.Points(:, 2);

E = edges(finalTria); % 三角剖分边缘
isEven = rem(E, 2) == 0; % 忽略边界边缘
Eeven = E(any(isEven, 2), :);
isOdd = rem(Eeven, 2) ~= 0;
Eodd = Eeven(any(isOdd, 2), :);

xMidpoints = ((xPoints((Eodd(:, 1))) + xPoints((Eodd(:, 2)))) / 2); % x 中点坐标
yMidpoints = ((yPoints((Eodd(:, 1))) + yPoints((Eodd(:, 2)))) / 2); % y 中点坐标
PMidpoints = [xMidpoints, yMidpoints]; % 中点坐标

中心点插值

最后，为了使获得的路径足够光滑，还需要在中心点之间进行插值，插值点的数量由变量 interpolationNum 控制：

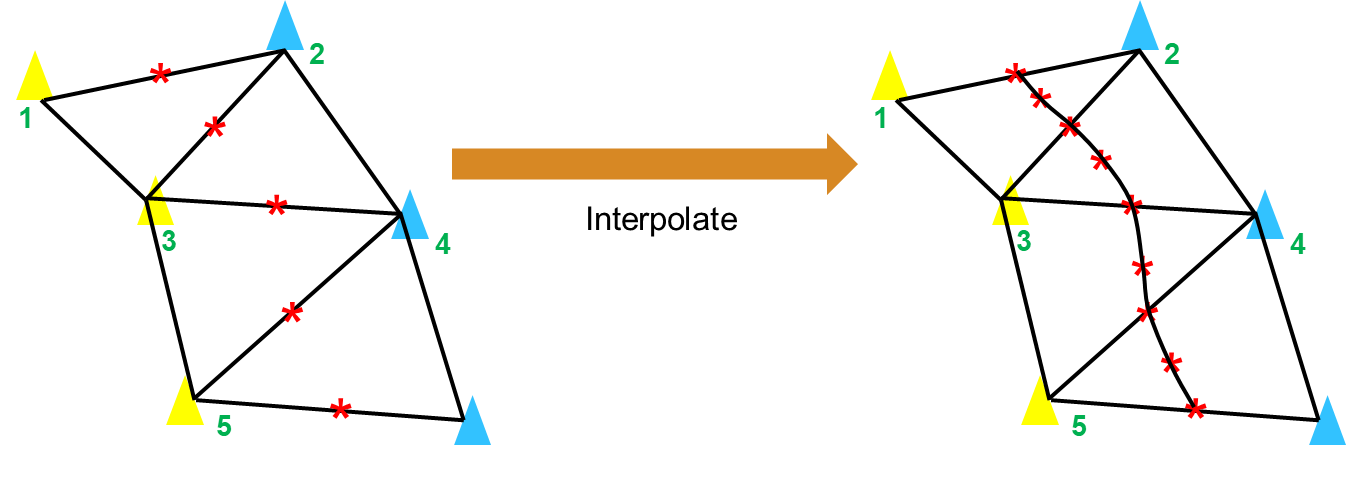
内边中心点插值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
%% 中心点插值
distancematrix = squareform(pdist(PMidpoints));
distancesteps = zeros(length(PMidpoints) - 1, 1);

for j = 2:length(PMidpoints)
    distancesteps(j - 1, 1) = distancematrix(j, j - 1);
end

totalDistance = sum(distancesteps); % 总经过距离
distbp = cumsum([0; distancesteps]); % 每个路径点间的距离
gradbp = linspace(0, totalDistance, interpolationNum); % 线性间距向量
xq = interp1(distbp, xMidpoints, gradbp, 'spline'); % 插值 x 坐标
yq = interp1(distbp, yMidpoints, gradbp, 'spline'); % 插值 y 坐标

startCount = (i / interval - 1) * interpolationNum + 1;
endCount = i / interval * interpolationNum;
xPos(:, startCount:endCount) = xq; % 在每次迭代后存储获得的 x 中点
yPos(:, startCount:endCount) = yq; % 在每次迭代后存储获得的 y 中点

期望路径可视化

对最终规划结果进行可视化：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
    % 动态绘制路径规划
    figure(3)
    % 用于展示规划路径全貌的子图
    pos1 = [0.1, 0.15, 0.5, 0.7];
    subplot('Position', pos1)
    pathPlanPlot(innerConePosition, outerConePosition, ...
        P, delaTria, finalTria, xMidpoints, yMidpoints, cIn, cOut, xq, yq)
    title(['Path planning based on constrained Delaunay' ...
               newline ' triangulation'])

    % 用于展示规划路径局部细节的子图
    pos2 = [0.7, 0.15, 0.25, 0.7];
    subplot('Position', pos2)
    pathPlanPlot(innerConePosition, outerConePosition, ...
        P, delaTria, finalTria, xMidpoints, yMidpoints, cIn, cOut, xq, yq)
    xlim([min(min(xPoints(1:2:(mc - 1)), xPoints(2:2:mc))) ...
              max(max(xPoints(1:2:(mc - 1)), xPoints(2:2:mc)))])
    ylim([min(min(yPoints(1:2:(mc - 1)), yPoints(2:2:mc))) ...
              max(max(yPoints(1:2:(mc - 1)), yPoints(2:2:mc)))])

end

% figure(3)的图例
h = legend('blueCone', 'redCone', 'start', 'midpoint', 'internal edges', ...
'inner boundary', 'outer boundary', 'planned path');

plannedPath = [xPos', yPos']; % 组合出最终规划路径

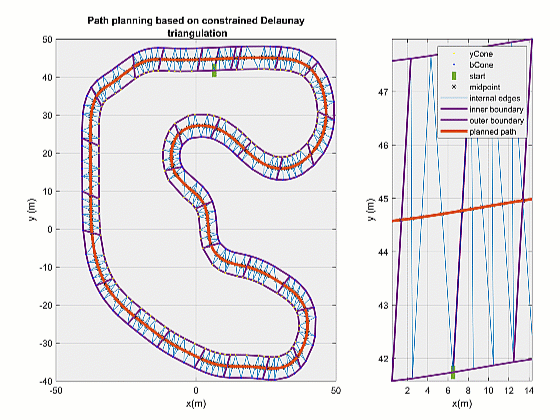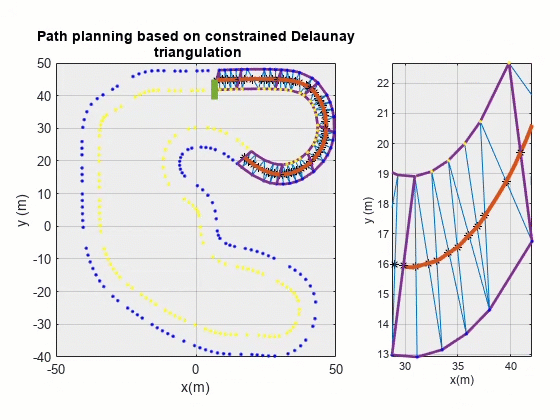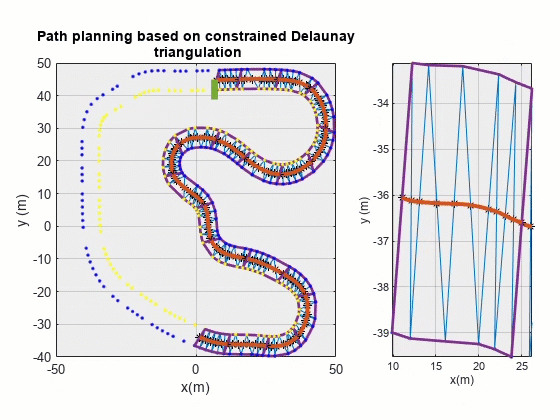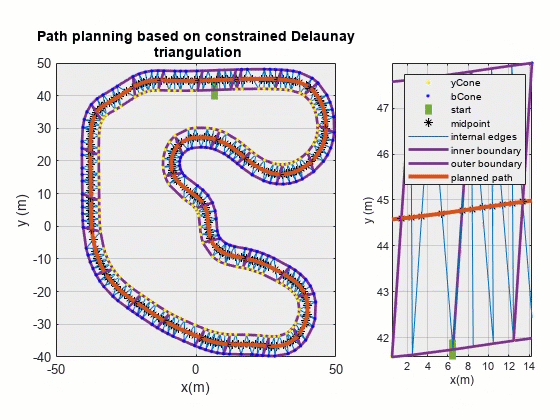
动态演示规划效果

其中 pathPlanPlot() 函数代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
% 动态绘图函数
function [] = pathPlanPlot(innerConePosition, outerConePosition, P, DT, TO, xmp, ymp, cIn, cOut, xq, yq)

    plot(innerConePosition.x_coor, innerConePosition.y_coor, '.b', 'MarkerFaceColor', 'b')
    hold on
    plot(outerConePosition.x_coor, outerConePosition.y_coor, '.r', 'MarkerFaceColor', 'r')
    plot(P(1, 1), P(1, 2), '|', 'MarkerEdgeColor', '#F57F4B', 'MarkerSize', 15, 'LineWidth', 5)
    grid on
    ax = gca;
    ax.GridColor = [0, 0, 0]; % [R, G, B]
    xlabel('x(m)')
    ylabel('y (m)')
    set(gca, 'Color', '#EEEEEE')

    hold on
    plot(xmp, ymp, '*k')
    drawnow

    hold on
    triplot(TO, 'Color', '#00AAAA') % 三角网格
    drawnow

    hold on
    plot(DT.Points(cOut', 1), DT.Points(cOut', 2), ...
        'Color', '#E54E5D', 'LineWidth', 2) % 左侧锥桶边界线
    plot(DT.Points(cIn', 1), DT.Points(cIn', 2), ...
        'Color', '#037CD2', 'LineWidth', 2) % 右侧锥桶边界线
    drawnow

    hold on
    plot(xq, yq, 'Color', '#927FD3', 'LineWidth', 2.5) % 期望路径
    drawnow

end

Figure_3

算法
#自动驾驶 #FSAE
基于 Delaunay 三角剖分的 FSAE 路径规划算法
https://muzing.top/posts/5b50f9b9/
作者
Muzing
发布于
2023年1月28日
更新于
2023年3月6日
许可协议