自动控制原理基础-03-频率特性

频率特性是控制系统在频率域中的数学模型。应用频率特性来分析系统的动态性能的方法，在控制理论中称为频率响应分析法或频率特性分析法。

对于那些很难从解析方法得到动态方程，但系统的频率特性可通过实验容易准确地获得的系统，频率响应分析法具有特别重要的意义。

第一节 概述

频率响应和频率特性

系统的频率响应：系统对正弦输入信号的稳定响应。

若系统输入正弦信号为：

$$x_i (t) = A_i \sin \omega t$$

则系统稳定输出为：

$$x_o (t) = A_o (\omega) \sin {[\omega t + \varphi(\omega)]}$$

• 幅频特性：$A(\omega) = A_o(\omega) / A_i$ ，稳定输出与输入的幅值比
• 相频特性：$\varphi (\omega) = [\omega t + \varphi(\omega)] - \omega t$ ，稳定输出与输入的相位差
• 系统的频率特性：$G(j \omega)$ ，系统输入正弦信号时，其稳态输出与输入的复数比，$A(\omega)$ 为其模，$\varphi (\omega)$ 为其幅角

将频率特性 $G(j \omega)$ 分解为实部和虚部，即

$$G(j \omega) = P(\omega) + jQ(\omega)$$

• 实频特性：$P(\omega)$
• 虚频特性：$Q(\omega)$

$$G(j \omega) = A(\omega) [\cos \varphi (\omega) + j \sin \varphi (\omega)]$$

应用欧拉公式，得

$$G(j \omega) = A(\omega) e^{j \varphi(\omega)}$$

频率特性的求取方法

1. 根据已知系统的微分方程，把输入量以正弦函数带入，求输出量的稳态解，取输出量的稳态分量与输入正弦信号的复数比求得；
2. 根据系统的传递函数来求取；
3. 通过实验测得。

介绍根据传递函数来求取频率特性的方法：

对于线性定常系统：

$$a_n \frac{\mathrm{d}^n x_o (t)}{\mathrm{d} t^n} + a_{n-1} \frac{\mathrm{d}^{n-1} x_o (t)}{\mathrm{d} t^{n-1}} + \cdots + a_1 \frac{\mathrm{d} x_o (t)}{\mathrm{d} t} + a_0 x_o(t) \\ \\ = b_m \frac{\mathrm{d}^m x_i (t)}{\mathrm{d} t^m} + b_{m-1} \frac{\mathrm{d}^{m-1} x_i (t)}{\mathrm{d} t^{m-1}} + \cdots + b_1 \frac{\mathrm{d} x_i (t)}{\mathrm{d}t} + b_0 x_i (t) \quad (n \geq m)$$

其传递函数为

$$G(s) = \frac{b_m s^m + b_{m-1} s^{m-1} + \cdots + b_1 s + b_0}{a_n s^n + a_{n-1} s^{n-1} + \cdots + a_1 s + a_0}$$

可以证明，将式中的 $s$ 以 $j \omega$ 替代，就可以得到系统的频率特性，即

$$G(j \omega) = G(s) \Big|_{s = j\omega} = \frac{b_m (j \omega)^m + b_{m-1} (j \omega)^{m-1} + \cdots + b_1 (j \omega) + b_0}{a_n (j \omega)^n + a_{n-1} (j \omega)^{n-1} + \cdots + a_1 (j \omega) + a_0}$$

频率特性的表示方法

1. 幅频特性图和相频特性图
2. 幅相频率特性图：也称奈奎斯特图
3. 对数频率特性图：也称波德图
4. 对数幅向频率特性图：也称尼柯尔斯图
5. 实频特性图和虚频特性图

第二节 幅相频率特性图——奈奎斯特图

在频率响应分析法中，常以闭环系统的开环传递函数对应的开环频率特性来分析闭环系统的品质，并据此判断闭环系统的稳定性。系统的开环传递函数 $G(s) H(s)$ 是由若干典型环节组成。

奈奎斯特（Nyquist）图

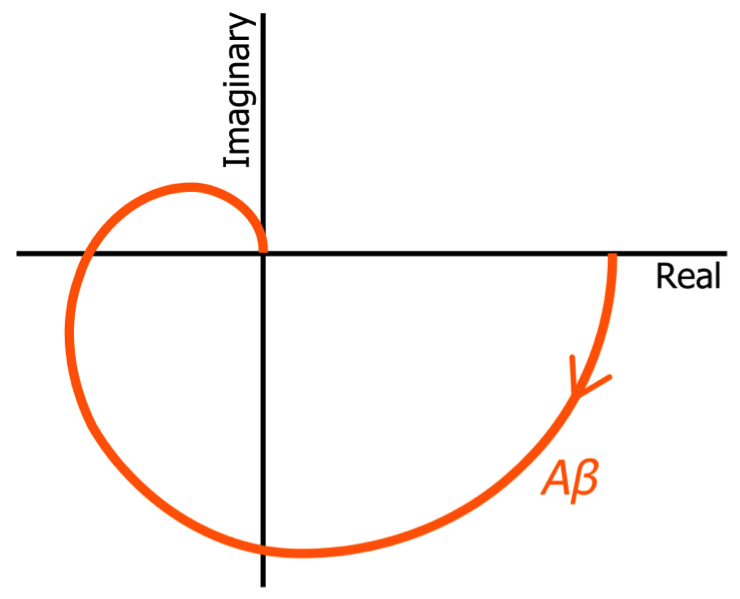
奈奎斯特图，也称幅相频率特性图、系统频率特性的极坐标图

系统的频率特性 $G(j \omega)$ 是 $\omega$ 的复变函数，当 $\omega$ 从零逐渐增大到无穷大时，矢量 $G(j \omega)$ 的端点在复平面上的轨迹所形成的曲线，称为幅相频率特性图。

典型环节的奈奎斯特图

比例环节

频率特性：

$$G(j \omega) = K$$

$$\varphi(\omega) = \angle G(j \omega)= 0^{\circ}$$

复平面实轴上的一个点 $(K, j0)$

积分环节

频率特性：

$$G(j \omega) = \frac{1}{j \omega} = 0 - j\frac{1}{\omega}$$

$$\varphi (\omega) = \angle G (j \omega) = - 90^{\circ}$$

与负虚轴重合的一条直线，当 $\omega = 0 \to \infty$ 时，它从负虚轴的无穷远趋近于原点 $O$。

积分环节也称为纯滞后环节。

理想积分环节

$$G(j \omega) = j \omega$$

与正虚轴重合的一条直线，当 $\omega = 0 \to \infty$ 时，它从原点 $O$ 趋近于正虚轴的无穷远。

理想积分环节也称为纯超前环节。

惯性环节

频率特性：

$$G(j \omega) = \frac{1}{1 + j \omega T}= \frac{1}{1 + \omega^2 T^2} - j \frac{\omega T}{1 + \omega^2 T^2}$$

$$\varphi (\omega) = \angle G (j \omega) = - \arctan (\omega T)$$

一个圆心在 $(\frac{1}{2} , j0)$ 点，半径为 $\frac{1}{2}$ 的半圆，在复平面右下半平面上

惯性环节的幅频特性随输入信号频率的增大而减小；相位滞后量随输入信号频率增大而增大，最大滞后量不超过90°

振荡环节

频率特性：

$$G(j \omega) = \frac{1}{1 - \omega^2 T^2 + j 2 \zeta \omega T} = \frac{1 - \omega^2 T^2}{(1 - \omega^2 T^2)^2 + (2 \zeta \omega T)^2} - j \frac{2 \zeta \omega T}{(1 - \omega^2 T^2)^2 + (2 \zeta \omega T)^2}$$

$$\varphi (\omega) = \angle G (j \omega) = - \arctan \frac{2 \zeta \omega T}{1 - \omega^2 T^2}$$

1. 对于一个固定的阻尼比 $\zeta$ 值，当 $\omega$ 从 0 变到无穷大时，振荡环节的奈奎斯特图的幅值从 $1 \to 0$ ；相角从 $0^{\circ} \to -180^{\circ}$。
2. 振荡环节的奈奎斯特图的形状与阻尼比 $\zeta$ 有关。在同一个频率下，其幅值随 $\zeta$ 的减小而加大。
3. 当 $\omega = \frac{1}{T}$ 时，$\varphi (\frac{1}{T})$ 恒为 $-90^{\circ}$ ，即奈奎斯特图和负虚轴的交点处的频率为 $\omega = \frac{1}{T} = \omega_n$ ，$\omega_n$ 是系统的无阻尼固有频率。
4. 在 $\zeta < \sqrt{2} / 2$ 的情况下，当 $\omega = \omega_r = \omega_n \sqrt{1 - 2 \zeta^2}$ 时，其幅值为最大，该频率称为振荡环节的谐振频率 ，与之相对应的最大幅值 $A(\omega_r)$ 称为振荡环节的谐振峰值

谐振峰值 $A(\omega_r)$ ：

$$A(\omega_r) = \frac{1}{2 \zeta \sqrt{1 - \zeta^2}}$$

一阶微分环节

$$G(j \omega) = 1 + j \omega T$$

$$\varphi (\omega) = \angle G (j \omega) = \arctan (\omega T)$$

由$(1, j0)$ 点开始平行于虚轴的一根向上的直线

二阶微分环节

$$G(j \omega) = 1 - \omega^2 T^2 + j 2 \zeta \omega T$$

系统开环频率特性的奈奎斯特图

系统开环频率特性奈奎斯特图的绘制

系统的开环频率特性的幅值等于各组成环节频率特性幅值的乘积，其相角为各组成环节的相角之代数和。

系统的开环奈奎斯特图的形状特点

其开环传递函数一般可以写成

$$G(s) = \frac{K Q_m (s)}{s^\nu P_{n - \nu} (s)}$$

字母符号	含义
$K$	系统的开环放大系数或增益
$\nu$	系统的开环传递函数中积分环节的个数（$\nu$ = 0，1，2，…）
$Q_m (s)$	$s$ 的 $m$ 次多项式
$P_{n - \nu}$	$s$ 的 $n - \nu$ 次多项式，$n \geq m$

• $0$ 型系统
  • 系统的开环传递函数中不包含积分环节（$\nu = 0$）的系统
  • 奈奎斯特图由正实轴上一个有限值$(K, j0)$ 开始，并以 $-(n - m) \times 90^{\circ}$ 的相角结束趋于原点结束
• $\rm{I}$ 型系统
  • 奈奎斯特图由 $(P_0, -j \infty)$ 开始，并以 $\varphi (\omega) = -(n - m) \times 90^{\circ}$ 的相角趋于原点结束
  • 与虚轴平行并经过 $(P_0, j0)$ 的直线为其奈奎斯特图的低频渐近线
• $\rm{II}$ 型系统
  • 奈奎斯特图起始于 $(- \infty, \pm j \infty)$ ，并以 $\varphi (\omega) = -(n - m) \times 90^{\circ}$ 的相角趋于原点结束

第三节 对数频率特性图——波德图

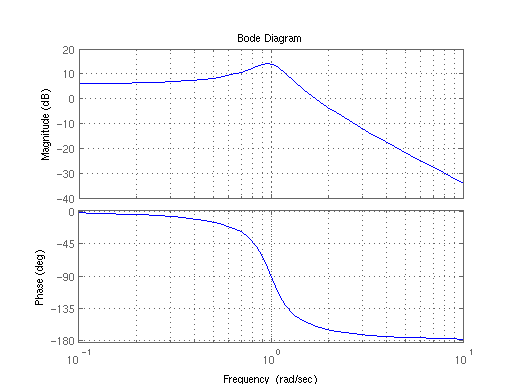
波德（Bode）图及其坐标轴的分度

波德图 = 对数幅频特性图 + 对数相频特性图

以频率为横轴，单位为弧度/秒（rad/s），按对数分度

典型环节的波德图

比例环节

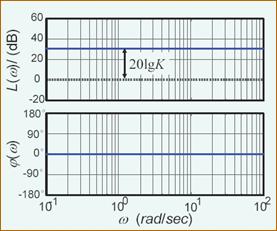
对数幅频特性：

$$L(\omega) = 20 \lg A (\omega) = 20 \lg K$$

对数幅频特性图为幅值等于 $20 \lg K$ 的一条水平线

对数相频特性：

$$\varphi_L (\omega) = \varphi(\omega) = 0^{\circ}$$

对数相频特性图：与横轴重合的一条直线

积分环节和理想微分环节

积分环节

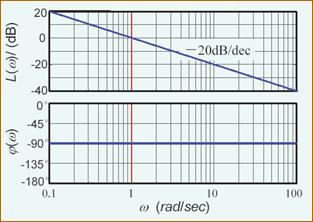
对数幅频特性：

$$L(\omega) = 20 \lg A(\omega) = -20 \lg \omega$$

对数幅频特性图：通过 $(1, 0)$ 点，斜率为 -20dB/dec 的直线，穿越频率 $\omega_c$ = 1

对数相频特性：

$$\varphi_L (\omega) = \varphi(\omega) = - 90^{\circ}$$

对数相频特性图：一条恒等于 -90° 的直线

穿越频率（增益交界频率）$\omega_c$ ：对数幅频特性图与横轴（0dB线）的交点处的频率

理想微分环节

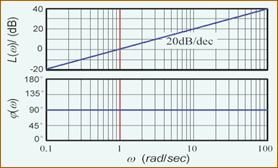
对数幅频特性：

$$L(\omega) = 20 \lg A(\omega) = 20 \lg \omega$$

对数幅频特性图：通过 $(1, 0)$ 点，斜率为 20dB/dec 的直线，穿越频率 $\omega_c$ = 1

对数相频特性：

$$\varphi_L (\omega) = \varphi(\omega) = 90^{\circ}$$

对数相频特性图：一条恒等于 90° 的直线

惯性环节和一阶微分环节

惯性环节

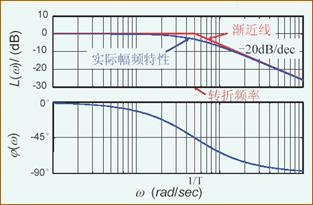
对数幅频特性：

$$L(\omega) = 20 \lg A (\omega) = -20 \lg \sqrt{1 + \omega^2 T^2}$$

对数相频特性：

$$\varphi_L (\omega) = \varphi (\omega) = -\arctan (\omega T)$$

低频渐近线：一条幅值为 0 dB 的水平线

高频渐近线：一条斜率为 -20 dB/dec 的经过 $(\frac{1}{T}, 0)$ 点的直线

转折频率 $\omega_T$ （交界频率）：两条渐近线相交处的频率，$\omega_T = \frac{1}{T}$

近似作图法：用低频渐近线和高频渐近线来分段近似表示其对数幅频特性图

惯性环节具有低通滤波器的作用

一阶微分环节

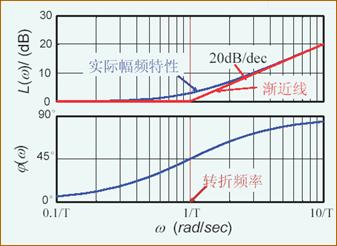
对数幅频特性：

$$L(\omega) = 20 \lg A (\omega) = 20 \lg \sqrt{1 + \omega^2 T^2}$$

对数相频特性：

$$\varphi_L (\omega) = \varphi (\omega) = \arctan (\omega T)$$

振荡环节与二阶微分环节

振荡环节

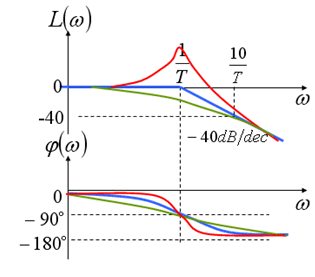
对数幅频特性：

$$L (\omega) = 20 \lg A (\omega) = -20 \lg \sqrt{(1 - \omega^2 T^2)^2 + (2 \zeta \omega T)^2}$$

对数相频特性：

$$\varphi_L (\omega) = \varphi (\omega) = - \arctan (\frac{2 \zeta \omega T}{1 - \omega^2 T^2})$$

谐振峰值：

$$20 \lg A (\omega_r) = 20\lg \frac{1}{2 \zeta \sqrt{1 - \zeta^2}}$$

此时的频率称为谐振频率 $\omega_r$

最佳阻尼比：$\zeta$ = 0.707（即 $\sqrt{2}/2$），此时对数幅频特性曲线和对数相频特性曲线在低频段近于直线。这对于测试仪器的设计很有好处，可以使仪器在线性段工作，并且测试仪器的复现能力强、跟踪能力好

二阶微分环节

对数幅频特性：

$$L (\omega) = 20 \lg A (\omega) = 20 \lg \sqrt{(1 - \omega^2 T^2)^2 + (2 \zeta \omega T)^2}$$

对数相频特性：

$$\varphi_L (\omega) = \varphi (\omega) = \arctan (\frac{2 \zeta \omega T}{1 - \omega^2 T^2})$$

系统的开环波德图

分别绘出各典型环节的对数幅频特性和对数相频特性图，然后分别相加即可得到

绘制开环波德图的步骤：

1. 把系统传递函数化为典型环节传递函数乘积的形式，分析其组成环节
2. 求出各转折频率，并由小到大排列为 $\omega_{T1}$ ，$\omega_{T_2}$ ，$\omega_{T_3}$，，$\cdots$ ，并在频率轴上将它们标出
3. 绘制系统的对数幅频特性图的低频渐近线。即在 $\omega < \omega_{T1}$ 时，绘制一条经过点 $(1, 20 \lg K)$ ，斜率为 $-20 \nu$ dB/dec 的直线。其中 $K$ 为系统开环放大系数， $\nu$ 为系统开环传递函数所包含的积分环节的个数。
4. 在每个转折频率处改变渐近线频率
   • 在惯性环节后，斜率减小 20 dB/dec
   • 在振荡环节后，斜率减小 40 dB/dec
   • 在一阶微分环节后，斜率增加 20 dB/dec
   • 在二阶微分环节后，斜率增加 40 dB/dec
5. 如有需要，可以通过对渐近线的修正，绘出准确的对数幅频特性图
6. 绘制各环节的对数相频特性图，然后将它们的相角在相同频率下代数相加，即可绘出系统完整的对数相频特性图

特点：

1. 对数幅频特性图和对数相频特性图各段间有对应的关系
2. 系统的开环对数幅频特性的渐近线是单调下降的
3. 系统的对数幅频特性渐近线各段斜率为 0 dB/dec 或 ±20 dB/dec 的整倍数

最小和非最小相位系统

最小相位传递函数：$G(s)$ 的所有零点和极点均在 $[s]$ 平面的左半平面及虚轴上

最小相位系统：具有最小相位传递函数的系统

第四节 频率特性的实验测定法

可以用频率特性实验分析法来确定那些用解析法难以分析的系统的数学模型

频率特性的实验分析方法

一般步骤：

1. 通过对所要识别系统进行频率特性实验获得系统的波德图
2. 用斜率为 0 dB/dec ， ±20 dB/dec ，±40 dB/dec 等的直线逼近实验得到的对数幅频特性曲线
3. 由对数幅频特性曲线的渐近线来确定系统的频率特性

由波德图确定（或估计）系统的频率特性

确定系统的类型及估计增益 $K$

最小相位系统频率特性的估算

一般步骤：

1. 作实验曲线的渐近线
2. 根据低频段渐近线的斜率确定系统的类型，低频段渐近线的斜率为 0 时，是 0 型系统；斜率为 $-20$ dB/dec 时，是 $\rm{I}$ 型系统；斜率为 $-40$ dB/dec 时，是 $\rm{II}$ 型系统；
3. 根据系统的类型和低频段渐近线与 0 dB 线的交点处的频率 $\omega$ 值，可以估算系统的增益 $K$